La elipse, como curva geométrica, fue estudiada por Menaechmus, investigada por Euclides, y su nombre se atribuye a Apolonio de Perge. El foco y la directriz de la sección cónica de una elipse fueron estudiadas por Pappus. En 1602, Kepler creía que la órbita de Marte era ovalada, aunque más tarde descubrió que se trataba de una elipse con el Sol en un foco. De hecho, Kepler introdujo la palabra «focus» y publicó su descubrimiento en 1609. Halley, en 1705, demostró que el cometa que ahora lleva su nombre trazaba una órbita elíptica alrededor del Sol.[2]
[editar] Elementos de una elipse
La elipse posee un «eje mayor», trazo AB (que equivale a  ), y un «eje menor», trazo CD (que equivale a
), y un «eje menor», trazo CD (que equivale a 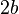 ); la mitad de cada uno de esos ejes recibe el nombre de «semieje», de tal manera que se los denomina «semieje mayor» y «semieje menor», respectivamente.
); la mitad de cada uno de esos ejes recibe el nombre de «semieje», de tal manera que se los denomina «semieje mayor» y «semieje menor», respectivamente.
 ), y un «eje menor», trazo CD (que equivale a
), y un «eje menor», trazo CD (que equivale a 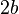 ); la mitad de cada uno de esos ejes recibe el nombre de «semieje», de tal manera que se los denomina «semieje mayor» y «semieje menor», respectivamente.
); la mitad de cada uno de esos ejes recibe el nombre de «semieje», de tal manera que se los denomina «semieje mayor» y «semieje menor», respectivamente.Sobre el «eje mayor» existen dos puntos  y
y  que se llaman «focos».
que se llaman «focos».
 y
y  que se llaman «focos».
que se llaman «focos».El punto  es uno que pertenezca a la «elipse».
es uno que pertenezca a la «elipse».
 es uno que pertenezca a la «elipse».
es uno que pertenezca a la «elipse».[editar] Puntos de una elipse
Si F1 y F2 son dos puntos del plano y d es una constante mayor que la distancia F1 F2, un punto Q pertenecerá a la elipse, si:
donde 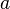 es el semieje mayor de la elipse.
es el semieje mayor de la elipse.
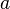 es el semieje mayor de la elipse.
es el semieje mayor de la elipse.[editar] Ejes de una elipse
Eje mayor (2 a) es la distancia mayor entre dos puntos adversos. En la figura, longitud del segmento AB.
La medida a es la mitad del eje mayor, o sea es el semieje mayor. La distancia del centro de la elipse al punto A o al punto B.
La medida a es la mitad del eje mayor, o sea es el semieje mayor. La distancia del centro de la elipse al punto A o al punto B.
El resultado constante de la suma de las distancias de cualquier punto a los focos equivale al eje mayor.
Obsérvese que d(AF2) + d (AF1) = d(AF2) + d (BF2)= AB
Obsérvese que d(AF2) + d (AF1) = d(AF2) + d (BF2)= AB
La medida b es la mitad del eje menor, o sea es el semieje menor, la distancia del centro al punto C o al punto D.
[editar] Excentricidad de una elipse
La excentricidad de una elipse es la razón entre su semidistancia focal (segmento que va del centro de la elipse a uno de sus focos), denominada por la letra 'c', y su semieje mayor. Su valor se encuentra entre cero y uno.
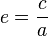 , con (0 < e < 1)
, con (0 < e < 1)
Dado que
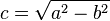 , también vale la relación:
, también vale la relación:o el sistema:
La excentricidad indica la forma de una elipse; una elipse será más redondeada cuanto más se aproxime su excentricidad al valor cero.[3]
[editar] Constante de la elipse
En una elipse, por definición, la suma de la longitud de ambos segmentos (azul + rojo) es una cantidad constante, la cual siempre será igual a la longitud del «eje mayor».
En la elipse de la imagen, la constante es 10. Equivale a la longitud medida desde el foco  al punto
al punto  (ubicado en cualquier lugar de la elipse) sumada a la longitud desde el foco
(ubicado en cualquier lugar de la elipse) sumada a la longitud desde el foco  a ese mismo punto
a ese mismo punto  . (El segmento de color azul sumado al de color rojo).
. (El segmento de color azul sumado al de color rojo).
 al punto
al punto  (ubicado en cualquier lugar de la elipse) sumada a la longitud desde el foco
(ubicado en cualquier lugar de la elipse) sumada a la longitud desde el foco  a ese mismo punto
a ese mismo punto  . (El segmento de color azul sumado al de color rojo).
. (El segmento de color azul sumado al de color rojo).El segmento correspondiente, tanto trazo 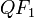 (color azul), como al
(color azul), como al 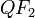 (color rojo), se llaman «radio vector». Los dos «focos» equidistan del centro
(color rojo), se llaman «radio vector». Los dos «focos» equidistan del centro  . En la animación, el punto
. En la animación, el punto 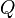 recorre la elipse, y en él convergen ambos segmentos (azul y rojo).
recorre la elipse, y en él convergen ambos segmentos (azul y rojo).
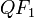 (color azul), como al
(color azul), como al 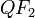 (color rojo), se llaman «radio vector». Los dos «focos» equidistan del centro
(color rojo), se llaman «radio vector». Los dos «focos» equidistan del centro  . En la animación, el punto
. En la animación, el punto 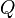 recorre la elipse, y en él convergen ambos segmentos (azul y rojo).
recorre la elipse, y en él convergen ambos segmentos (azul y rojo).[editar] Ecuaciones de la elipse
La ecuación de una elipse en coordenadas cartesianas, con centro en el origen, es:
donde a > 0 y b > 0 son los semiejes de la elipse (a corresponde al eje de las abscisas, b al eje de las ordenadas). El origen O es la mitad del segmento [FF']. La distancia entre los focos FF' se llama distancia focal y vale 2c = 2ea, siendo e la excentricidad y a el semieje mayor.
Si el centro de la elipse se encuentra en el punto (x1, y1), la ecuación es:
En coordenadas polares con origen en un de sus focos la ecuación de la elipse es:
En coordenadas polares con origen en su centro la ecuación de la elipse es:
La ecuación paramétrica de una elipse con centro en (h,k) es:
con  no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre α y θ es
no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre α y θ es
 no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre α y θ es
no es el ángulo θ del sistema de coordenadas polares con origen en el centro de la elipse (tampoco es el ángulo del sistema de coordenadas polares con origen en algún foco de la elipse). La relación entre α y θ es-
 .
.
[editar] Área interior de una elipse
El área de la superficie interior de una elipse es:
Siendo a y b los semiejes.[4]
[editar] Longitud de una elipse
El cálculo del perímetro de una elipse requiere del cálculo de integrales elípticas de segunda especie.
Sin embargo, el matemático Ramanujan ideó una ecuación más simple que se aproxima razonablemente a la longitud de la elipse, pero en grado menor que la obtenida mediante integrales elípticas. Ramanujan, en su formula, entre otros valores utiliza el “semieje mayor” y el “semieje menor”. Ecuación de la longitud de una elipse:
[editar] Propiedades notables
La elipse goza de ciertas propiedades asociadas a sus componentes, como se puede ver en Analogía de Michelson y Morley.
[editar] La elipse como cónica
La elipse surge de la intersección de una superficie cónica con un plano, de tal manera que la inclinación del plano no supere la inclinación de la recta generatriz del cono, consiguiendo así que la intersección sea una curva cerrada. En otro caso el corte podría ser una hipérbola o una parábola. Es por ello que a todas estas figuras bidimensionales se las llama secciones cónicas o simplemente cónicas.
[editar] La elipse como hipotrocoide
La elipse es un caso particular de hipotrocoide, donde R = 2r, siendo R el radio de la circunferencia directriz, y r el radio de la circunferencia generatriz.
En una curva hipotrocoide, la circunferencia que contiene al punto generatriz, gira tangencialmente por el interior de la circunferencia directriz.
[editar] Construcción paramétrica de una elipse
Se dibujan dos circunferencias concéntricas cuyos diámetros equivalen a la medida de los ejes ortogonales de la futura elipse. Si trazamos segmentos palalelos a los ejes principales X e Y, partiendo del extremo de los radios alineados, la intersección de dichos segmentos son puntos de la elipse.
[editar] Anamorfosis de un círculo en una elipse
Cierta trasformación de la circunferencia (al deformar ortogonalmente el plano cartesiano asociado a ella), se denomina anamorfosis. Se corresponde a una perspectiva especial. El término anamorfosis proviene del idioma griego y significa trasformar.
 Esta circunferencia se transforma en una elipse mediante una anamorfosis, donde el eje Y se ha contraído y el X se ha dilatado. |
En el caso de la circunferencia, si el plano cartesiano se divide en cuadrados, cuando dicho plano se «deforma» en sentido del eje X, el Y, o ambos, la circunferencia se transforma en una elipse, y los cuadrados en rectángulos.
[editar] Elipses semejantes
Se dice que dos figuras son semejantes cuando se diferencian sólo en el tamaño (pero no en la forma), de tal manera que multiplicando todas las longitudes por un factor dado, se pasa de una figura a la otra. Hay un teorema de utilidad en Física [5] acerca de la intersección de una recta con dos elipses semejantes y concéntricas.
Teorema: Si la intersección de una recta con la corona comprendida entre dos elipses semejantes con iguales centro y ejes consta de dos segmentos, entonces éstos tienen igual longitud.
Demostración: El teorema es cierto, por simetría, en el caso particular en que las elipses dadas sean dos circunferencias concéntricas. Contrayendo o dilatando uniformemente una de las direcciones coordenadas, podemos transformar cualquier caso en este caso particular. Al contraer o dilatar uniformemente una de las direcciones coordenadas todos los segmentos con la misma pendiente cambian su longitud en la misma proporción. Por tanto, puesto que al final del proceso los dos segmentos de la recta tienen la misma longitud, la tenían ya al principio. QED.
No deben confundirse las elipses semejantes con las elipses cofocales.




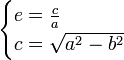

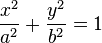





![P \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]\!\,](http://upload.wikimedia.org/math/4/5/3/4531867e543bc27be7c45f80a7599da1.png)




No hay comentarios:
Publicar un comentario